こんばんは。
やっと、期末テストが終わりました!
ターム制のおかげで期末テストが2つの期間に分かれたおかげで、少し勉強が楽になりましたが、少ないとは言ってもやはり1つ1つの内容が難しくて、大変でした。
今回はこの間、バイト終わりに買った缶から始まる記事を書いていきます。
1)ペプシ缶に穴が開いた・・・
まずはペプシ缶に穴が開いた話を。
僕はこの間、バイトが終わった後とても疲れていたので、近くの自販機でペプシを買う事にしました。(本当はコーラの方が好きですが、安くてたくさん入っていたので・・・(笑))
「疲れたぜ~。ペプシでも飲んで疲れを吹き飛ばすぜ!」
そう思って、自転車🚴を止めたその時・・・
ペプシ、落下!!!!
と、同時に・・・
ペプシ、破裂!!!!
ペプシのシャワーを浴びる羽目になりました。
熱かったので涼しくはなりましたが、全身、ベトベトになりました。
穴が開いたペプシ缶がこちら。

ドアの前で、少し、残ったコーラをちびちび飲みました。
2)ペプシ缶を洗った所・・・
飲み終わった後、台所でペプシ缶を洗っていた所、懐かしい現象を見ました。
大学生の方々、懐かしくないですか~?
たしか、穴を水面からの距離が大きいところに開けるほど、穴から出る水の到達距離は伸びるんでしたよね!
という事で、一体、どこまで水は噴射されるのかを理論的に計算した結果と実験値から求めていこうと思います!(笑)
3)理論値(水面の低下を無視した場合)
まず、流体についての力学的エネルギー保存則(ベルヌーイの定理)より、
![]()
ここで、V1,P1,Z1は下図の①面の速度,圧力,下面からの高さでV2,P2,Z2は②面の速度、圧力、下面からの高さです。
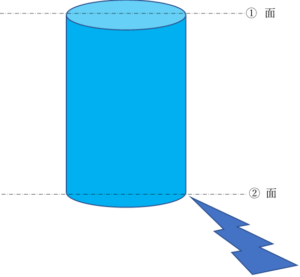
この時、V1=0,P1=P2=大気圧,Z1=h,Z2=0であるので、
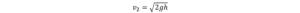
これは”トリチェリの定理”といいます。
*ペットボトルの断面積がペットボトルに開いた穴の断面積よりも十分に大きくて、水面の位置の変化が無視出来る。
とりあえず、水面の位置の変化を無視した上の方法でやっています!
計算した結果が以下のグラフ。
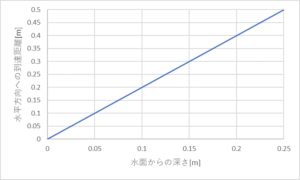
4)実験方法
実験方法としてはまず、下の動画のような「色水戦法」を考えました。
しかし、この方法は色水が染みわたってしまって測定不能になってしまったので・・・
以下の「ベンチプレス法」に変えました。
5)実験
お待たせしました!
いよいよ、実験です!
実験はペプシ缶の穴が大きすぎたので、高さh=0.25[m]、入り口0.25[m^2]にくりぬいたペットボトルで行いますm(__)m。
まず、トリチェリの定理で求めた理論値と実験値を調べました。
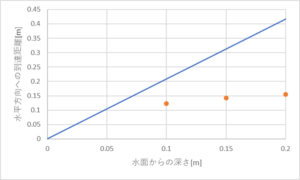
*プロットしてあるのが実験値です。
測定は水面から0.05、0.1、0.15、0.20[m]の所で行いました。
その内、0.05[m]の所からは大気圧に押され、水が出てきませんでした。
6)考察
上の結果は理論値とかなりかけ離れていたので、ペットボトルの中身に摩擦損失ヘッドが生じていたと考えました。
すると、ベルヌーイの式は以下のように。
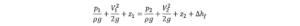
Δhfは管摩擦損失です。
すると、V2は・・・
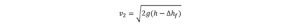
ここで、Δhfは以下のように表せることを思い出します。
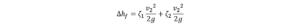
ここで、第1項は入口損失でζは入り口損失係数でペットボトルの穴の形状的にζ1=0.06です。第2項は出口損失で出口損失係数ζ2=1です。
そして、上の2つの式を使っていろいろと計算すると・・・
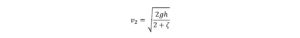
となりました。
これをグラフ化すると・・・
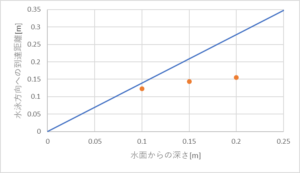
こんな感じになりました。
少し、理論値と実験値が近くなりました。
でも、これでもやはり少し差異がありましたよね。
その原因として僕が考えたのが、以下の2点。
①実験中、水を継ぎ足すべきではなかった。
②体積流量Q[m^3/s]を測って、平均流速を求めて管摩擦損失を含めるべき。
いかがでしたでしょうか?
僕はここらへんで、飽きてきたので①、②の改善をした実験はもうしませんが、この記事を読んで、これを自由研究にしてみようと思った方は①、②の改善をして実験をしてみて下さい。
放り投げて、m(_ _)mゴメン。
僕的には夏で扱ったこともあり、実験中に水の音を聞いているだけで涼しい気分を味わえたので非常に楽しい実験でした。
実験自体は2時間くらい終わるので、おすすめの自由研究です。
ぜひ!!
▲▲▲アリガ島▲▲▲
「未定」