こんにちは～
”電圧”って、たしか小学生4年生の頃くらいに初めて習ってから中学、高校とずっと物理の時間に出てきましたよね～。
”電圧”について最も有名な式は以下の式(1)”オームの法則”でしょうか。
これを使って電圧降下Vをずっと求めてきましたよね～。
でも、よく考えたら”抵抗”以外の”コイル”や”コンデンサ”という要素では電圧低下は起こらないのでしょうか？
・・・
実は起こります！
でも、それは高校まででは無視されて来ました。
ということで、今回は大学生の自分がそれを無視せずに、抵抗以外の要素ではいったいどのくらい電圧降下が起きているのかをしっかり紹介しようと思います！
全ての要素で、意外な共通点も明らかになるのでぜひ、ここでやめずにお読みください！
題：交流回路による電圧低下と回路方程式
１）抵抗
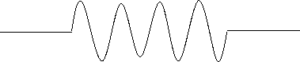
電流i(t)が流れたとすると、式(1)のようになります。
・電圧降下：
ここで、R：抵抗値[Ω]です。
これが有名な”オームの法則”ですね！
２）コイル
電流i(t)が流れたとすると、式(2)のようになります。
・電圧降下：
ここで、L：インダクタンス[H]です。
この式からコイルでの電圧降下は電流の時間変化(微分)に比例することが分かります。
つまり、乾電池などの直流電流は電流の時間変化が無いので、コイルに電流を流しても電圧降下はないという事になります。
３）コンデンサ
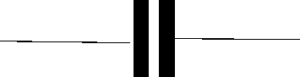
電流i(t)が流れたとすると、式(3)のようになります。
・電圧降下：
ここで、C[F]：キャパシタンスです。
この式からコンデンサでの電圧降下は電流の時間変化(積分)に比例することが分かります。
４）使用例
以上の回路素子の電圧降下は具体的にはどのように使うのでしょうか？
なんか、電圧降下は今までは”オームの法則”だけを使って簡単に解くもので仲良くやっていたのに、”微分”とか”積分”とかの難しい要素が加わって”電圧降下”を求めるのが遠い存在になっちゃったな～。
って、思っちゃいました？
確かに、僕も最初はそう思いました。
でも、今では1)～3)式を使えば電気の分野をより深く知れ、”電気”が面白い分野を面白くするものだと理解しています。
という事で、”電圧降下”を嫌いになっちゃわないように、その使用例である”RLC直列回路”を紹介したいと思います！
新しい事って何に使うのか分からないと全く面白くないと思うので・・・
図1のRLC直列回路について方程式を立てると、式(4)のようになります。
図1．RLC直列回路
ここで、起電力：e(t)[V]、電流：i(t)[A]であるとします。
すると・・・
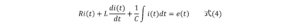となります。
大学で数学を習ったことがある方はわかると思いますが、これは微分方程式といって、手順を踏めば電流値I(t)が計算でき、それを用いればすべての回路素子での電圧降下が分かるという事になります！
これで、一見、難しそうな図1のRLC回路も丸裸にすることが出来ます！
題：RLC直列回路って？
R：電気抵抗[Ω]、L：自己インダクタンス[H]、C：電気容量[F]が交流電流に直列に接続された回路のことです！
いかがでしたでしょうか？
これまでよく1人で登場していた”オームの法則”は1人ではなかったんですね！
電流i(t)という媒介を微分したり、積分したりするだけですべての要素の電圧降下を求めることが出来るってすごいですよね～
そういえば、1)～3)式って、力学で”進んだ距離”、”速度”、”加速度”を求めた時に似てますよね～。(今、気づいた！)
高校で電気に挫折しかけてる高校生！
高校では難しい説明をはしょっているため、他にもかも暗記に頼るしかなくなり、”電気”が面白くなく感じているかもしれませんが、裏のこういう世界も知ると面白くなってくると思います。
まあ、こんなことばかりをやっていても点数が伸びないのがセンター試験、2次試験だと思いますが・・・
たまに息抜きと思ってやってみるいいのではないのでしょうか？
挫折せずに頑張って！(僕も”電気”の分野、大嫌いでした(笑))
「未定」
