こんにちは～
普段、何かを圧縮する機会って結構ありますよね！
空き缶をつぶしたり、ゴミ箱🚮の中にごみを押し込んだり・・・。
後はベンチに座っていて体重でベンチが壊れてしまわないか心配になったりすることなんてありません？
今回は機械屋さんがその圧縮がかかった時の材料について調べるために使っている試験法である”圧縮試験”について紹介します！
①圧縮試験
１）”応力”って？
”圧縮試験”の前に、”圧縮試験”について語るうえで欠かすことのできない”応力”についての説明をします。
”応力”とは単位面積当たりにかかる荷重のことで、一般的に式(１)で表されます
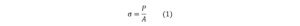
ここで、σ：応力[N/m^2]，P：荷重[N]，A：断面積[m^2]です。
ちなみに、
[N/m^2]=[Pa]
なので、”応力”とは”圧力”のことです。
でも、僕は
「なぜ、高校までみたいに普通に荷重Pで評価しないのか？」
「”応力”なんて高校までで１言も聞いたことがないぞなー！」
機械科に入学した当初、ずっとそう思っていて、3年生になるまでずっと”応力”という概念に疑問を持っていました。
でも、勉強するうちにわかってきて、この理由は面積Aで荷重Pを割ることにより、面積Aの大きさによる力の加わり方のfactorを取り除くためだと分かりました。
今では”応力”で評価しない時が不思議に思うレベルです。
では、この応力を実際に使っていきましょう！
いってみよう！！
”応力”とセットで重要な概念であるのが”応力ーひずみ線図”です。
それの代表的な図を下の図１にしめします。（大体、どれもこんな感じになります）
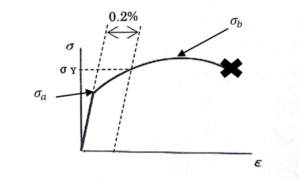図1．応力ーひずみ線図
ここで、横軸：ひずみε[-]，縦軸：応力σ[N/m^2]です。
この応力ひずみ線図は機械工学で”材料力学”を勉強しているとよく出てくる、機械科にとって非常に重要な図です。
図中に応力ーひずみ線図で読み取るべき記号を入れてあります。
それぞれ・・・
・σa：降伏応力（弾性領域での最大の応力）
・σy：耐力（0.2%の残留ひずみを生じるときの応力）
・σb：引っ張り強さ
・×：破断点(ここで材料は切れます)
となっています。
また、この図の読み取りで大事なことを追記しておきます。
・弾性領域：荷重を除した時、元の形に戻る領域のことで、σa(降伏応力)までのひずみ領域がこれにあたります。
・塑性領域：荷重を除した時、元の形に戻らない領域のことで、σa(降伏応力)以上でのひずみ領域がこれにあたります。
Q.では、以上の数値を機械屋さんがどう利用しているのか？
まず、基本的に使うのはσa(降伏応力)です。
この降伏応力までのひずみεが弾性領域であるので、これ以上のひずみを加えると材料が変形してしまいます。
つまり、少しでも変形したらまずい部品などはこれを参考にして作ります。
もちろん、この降伏応力のギリギリを狙って作るのではなく、”安全率”を各業界基準に合わせて降伏応力よりも何割か小さくなるように設計するそうです。次に、σb(引っ張り強さ)です。
σb(降伏応力)を超すと、変形してしまいますが、引っ張り強さ以下のひずみであれば破断することはありません。
つまり、破断しなければ変形しても大丈夫！っていうものを設計するときに使われます。
これは想像ですが、電車の線路は熱膨張して変形しても大丈夫なように作られているので、この時はσb(引っ張り強さ)を使っているのではないでしょうか？
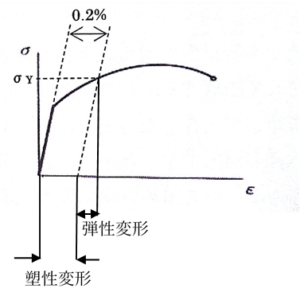図2．塑性領域塑性領域とは名前に騙されて、”塑性変形”しかしてないのではないか？と、思いがちですが、正しくは”塑性変形”と”弾性変形”が混在する領域”のことです。
降伏応力を過ぎた応力の場所から弾性領域の関数と同じ傾きで線（図2で、σ=0点まで繋いでいる点線）を引っ張った時、σ=0となった時のひずみε、ここまでは”弾性変形”で、底からε=0までのひずみ領域が”塑性変形”です。
以上のようなことを調べるのが機械系における”圧縮試験”になります。
あと、実際にやったら分かるのですが、同じ荷重をかけても材料の表面の状態で圧縮による材料の変容は大きく異なります。
もしかしたら、他の条件でも変わってくるのかも！！
面白くなってきました！
調べてみたら面白そうです。
いかがでしたでしょうか？
今回の説明が少しでも参考になれば嬉しいです！
”圧縮”・・・
なかなか奥が深そうです。
最後までお読みいただきありがとうございました。
✌
「未定」
