こんにちは~
前回の予告通り、今回は“行列の固有値と固有ベクトルを用いた行列の対角化”の中でも変換行列に直行行列を用いるもの。それも、もとは直交行列ではないものを無理やり直交行列にしたという特殊パターンついて書いていきたいと思います。
それでは~
シュワッチ!
第6回:【院試対策】線形代数⑥(固有値と固有ベクトルを用いた行列の対角化Part2)
第6回も”固有値と固有ベクトルを用いた行列の対角化”についてです。
でも、先にも書いた通り今回のは一癖ある特殊パターンです!
それは変換行列に直交行列を用いるパターンです。
前回の記事で紹介した通り、行列の対角化で用いる変換行列は必ずしも直交行列である必要はありません!
「じゃあ、何のために直行化するのか」って?
これについては僕もわかりません(笑)
でも、自分の大学院ではなぜか変換行列に直行行列を使わせたがります・・・
今回の計算で必要となる知識についての過去の記事はこちら↓
・【院試対策】線形代数③(行列の和積)
・【院試対策】線形代数④(行列の固有値と固有ベクトル)
・【院試対策】線形代数⑤(固有値と固有ベクトルを用いた行列の対角化Part1)
それでは今回も例題を使った演習で理解していきましょう♪
<例題1>
以下の行列Aを変換行列に直交行列を用いて、対角化せよ。
\[
A = \left(
\begin{array}{ccc}
2 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 2
\end{array}
\right)
\]
<解法>
\begin{equation}
AX = λX より、(A – λE)X = 0
\end{equation}
\[
ここで、T = A – λE = \left(
\begin{array}{ccc}
2 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 2
\end{array}
\right)
– \left(
\begin{array}{ccc}
λ & 0 & 0 \\
0 & λ & 0 \\
0 & 0 & λ
\end{array}
\right)
\]
\[
= \left(
\begin{array}{ccc}
2-λ & 1 & 1 \\
1 & 2-λ & 1 \\
1 & 1 & 2-λ
\end{array}
\right)
とおく。
\]
\begin{equation}
すると、TX = 0・・・①であり、
\end{equation}
\[
\mathrm{det}T = |T| = \left|
\begin{array}{ccc}
2 – λ & 1 & 1 \\
1 & 2 – λ & 1 \\
1 & 1 & 2 – λ
\end{array}
\right| = 0
となればいいことがわかる。
\]
\begin{equation}
= 1 + 1 + (2-λ)^3 – (2-λ) – (2-λ) – (2 -λ)
\end{equation}
\begin{equation}
= 2 + 8 -8λ+2λ^2-4λ+4λ^2-λ^3-6+3λ
\end{equation}
\begin{equation}
= -λ^3+6λ^2-9λ+4
\end{equation}
\begin{equation}
λ^3-6λ^2+9λ-4=0
\end{equation}
\begin{equation}
(λ-1)(λ^2-5λ+4) = 0
\end{equation}
\begin{equation}
(λ-1)^2(λ-4) = 0
\end{equation}
\begin{equation}
よって、固有値はλ = 1,4
\end{equation}
次にそれぞれの固有値における固有ベクトルを求めます。
\begin{equation}
ⅰ)λ = 1の時、①をT_{1}X_{1}=0,
\end{equation}
\[
X_{1}=\left(
\begin{array}{ccc}
α_{1} \\
α_{2} \\
α_{3}
\end{array}
\right)
とすると、
\]
\[
\left(
\begin{array}{ccc}
1 & 1 & 1\\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
α_{1}\\
α_{2}\\
α_{3}
\end{array}
\right)
= \left(
\begin{array}{ccc}
0\\
0\\
0
\end{array}
\right)
\]
\begin{equation}
α_{1} + α_{2} + α_{3} = 0
\end{equation}
\begin{equation}
α_{2}=k_{1},α_{3}=k_{2}とすると、α_{1}=-k_{1}-k_{2}より、固有ベクトルX_{1}は
\end{equation}
\[
X_{1}=k_{1}\left(
\begin{array}{ccc}
-1 \\
1 \\
0
\end{array}
\right)
+k_{2}\left(
\begin{array}{ccc}
-1 \\
0 \\
1
\end{array}
\right)
(k_{1},k_{2}\neq0)
\]
\begin{equation}
ⅱ)λ = 4の時、①をT_{2}X_{2}=0,
\end{equation}
\[
X_{2}=\left(
\begin{array}{ccc}
α_{4} \\
α_{5} \\
α_{6}
\end{array}
\right)
とすると、
\]
\[
\left(
\begin{array}{ccc}
-2 & 1 & 1\\
1 & -2 & 1 \\
1 & 1 & -2
\end{array}
\right)
\left(
\begin{array}{ccc}
α_{4}\\
α_{5}\\
α_{6}
\end{array}
\right)
= \left(
\begin{array}{ccc}
0\\
0\\
0
\end{array}
\right)
\]
\begin{eqnarray}
\begin{cases}
-2α_{4} + α_{5} + α_{6} = 0 & \\
α_{4} -2α_{5} + α_{6} = 0 \\
α_{4} + α_{5} – 2α_{6} = 0
\end{cases}
\end{eqnarray}
\begin{equation}
α_{5}=k_{3}とすると、α_{4}=-k_{3},α_{6}=k_{3}より、固有ベクトルX_{2}は
\end{equation}
\[
X_{2}=k_{3}\left(
\begin{array}{ccc}
1 \\
1 \\
1
\end{array}
\right)
(k_{3}\neq0)
\]
以上、ⅰ),ⅱ)より、
\[
変換行列P= \left(
\begin{array}{ccc}
-1 & -1 & 1 \\
1 & 0 & 1 \\
0 & 1 & 1
\end{array}
\right)
\]
これはそれぞれの列ベクトル同士を“行列の和積”を用いて計算すると、1列目と2列目の和積が0にならないので直行行列ではありません。
ですので、これをシュミットの正規直交化法を用いて直交化します!
\[
a_{1}=\left(
\begin{array}{ccc}
-1 \\
1 \\
0
\end{array}
\right)
,a_{2}=\left(
\begin{array}{ccc}
-1 \\
0 \\
1
\end{array}
\right)
,a_{3}=\left(
\begin{array}{ccc}
1 \\
1 \\
1
\end{array}
\right)
とおく。
\]
\begin{equation}
①u_{1}=\frac{1}{||a_{1}||}a_{1}
\end{equation}
\[
=\frac{1}{\sqrt{2}} \left(
\begin{array}{c}
-1 \\
1 \\
0
\end{array}
\right)
\]
\[
②b_{2} = a_{2} – \sum_{k=1}^1 (u_{k}・a_{2})u_{k}
\]
\begin{equation}
=a_{2}-(u_{1}・a_{2})u_{1}
\end{equation}
\[
=\left(
\begin{array}{ccc}
-1 \\
0 \\
1
\end{array}
\right)
– \frac{1}{2}
\left(
\begin{array}{ccc}
-1 \\
1 \\
0
\end{array}
\right)
\]
\[
=- \frac{1}{2} \left(
\begin{array}{ccc}
1 \\
1 \\
-2
\end{array}
\right)
\]
\begin{equation}
u_{2}=\frac{1}{||b_{2}||}b_{2}
\end{equation}
\[
=\frac{-1}{\sqrt{6}} \left(
\begin{array}{c}
1 \\
1 \\
-2
\end{array}
\right)
\]
\[
③b_{3} = a_{3} – \sum_{k=1}^2 (u_{k}・a_{3})u_{k}
\]
\begin{equation}
=a_{3}-{(u_{1}・a_{3})u_{1}+(u_{2}・a_{3})u_{2}}
\end{equation}
\[
=\left(
\begin{array}{ccc}
1 \\
1 \\
1
\end{array}
\right)
\]
\begin{equation}
u_{3}=\frac{1}{||b_{3}||}b_{3}
\end{equation}
\[
=\frac{1}{\sqrt{3}} \left(
\begin{array}{c}
1 \\
1 \\
1
\end{array}
\right)
\]
よって、変換行列Pは
\[
P= \left(
\begin{array}{ccc}
\frac{-1}{\sqrt{2}} & \frac{-1}{\sqrt{6}} & 1 \\
\frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{6}} & 1 \\
0 & \frac{2}{\sqrt{6}} & 1
\end{array}
\right)
と直交行列に変換できた。
\]
対角化した行列は
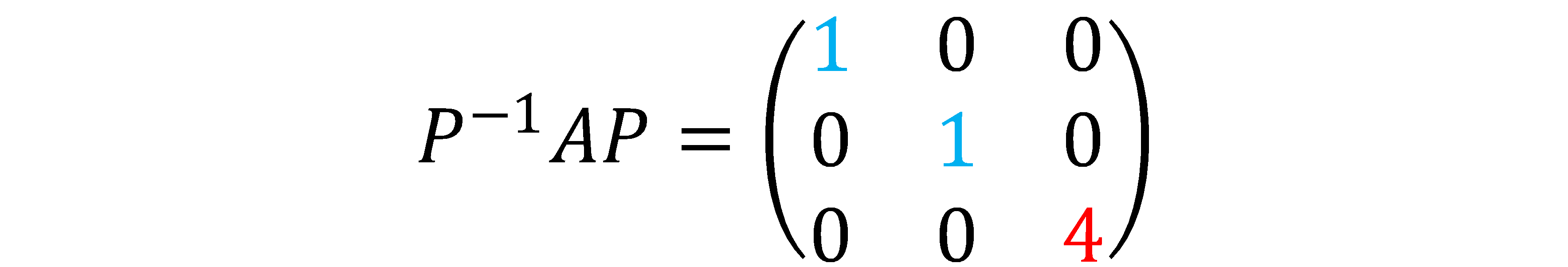
【シュミットの正規直行化法】
\begin{equation}
一般の基底(a_{1},a_{2},a_{3},・・・,a_{n})について、
\end{equation}
\begin{equation}
ⅰ)m = 1の時、
u_{1}=\frac{1}{||a_{1}||}a_{1}
\end{equation}
\[
ⅱ)2\le m\le nの時、
\]
\begin{equation}
b_{m} = a_{m} – \sum_{k=1}^{m-1} (u_{k}・a_{m})u_{k}
\end{equation}
\begin{equation}
u_{m}=\frac{1}{||b_{m}||}b_{m}
\end{equation}
以上より、シュミットの正規直交化法後の変換行列は
\begin{equation}
P=(u_{1},u_{2},・・・,u_{n})
\end{equation}
いかがでしたでしょうか?
この数式を書くのが中々時間がかかるので1問しか紹介できませんでしたが、上の例題で示した解法が直交行列ではないものを無理やり直交行列にした特殊パターンの基本的な求め方となります。(なんか、この書き方矛盾してるみたい(笑))
次回は逆行列の求め方について紹介いたします。
お楽しみに♪
▲▲▲アリガ島▲▲▲
「【院試対策】線形代数⑦(逆行列)」