【院試対策】線形代数⑤（固有値と固有ベクトルを用いた行列の対角化Part１）

こんにちは～

前回の予告通り、今回は“行列の固有値と固有ベクトルを用いた行列の対角化”について記事にしていきたいと思います。

それでは～

シュワッチ！

第5回：【院試対策】線形代数⑤（固有値と固有ベクトルを用いた行列の対角化）

第5回は”固有値と固有ベクトルを用いた行列の対角化”についてです。
前回の記事では行列の固有値と固有ベクトルの求め方について書きましたが、今回はそれらを用いた対角化について書いていきます！
前回の記事はこちら↓
・【院試対策】線形代数④（行列の固有値と固有ベクトル）

それでは今回も例題を使った演習で理解していきましょう♪

＜例題１＞
以下の行列Aを変換行列Pを用いて、対角化せよ。
\[
A = \left(
\begin{array}{ccc}
1 & 2 & 0 \\
2 & 1 & 0 \\
0 & 0 & 3
\end{array}
\right)
\]

＜解法＞
\begin{equation}
AX = λX　より、（A – λE）X = 0
\end{equation}

\[
ここで、T = A – λE = \left(
\begin{array}{ccc}
1 & 2 & 0 \\
2 & 1 & 0 \\
0 & 0 & 3
\end{array}
\right)
– \left(
\begin{array}{ccc}
λ & 0 & 0 \\
0 & λ & 0 \\
0 & 0 & λ
\end{array}
\right)
\]

\[
= \left(
\begin{array}{ccc}
1-λ & 2 & 0 \\
2 & 1-λ & 0 \\
0 & 0 & 3-λ
\end{array}
\right)
とおく。
\]

\begin{equation}
すると、TX = 0・・・①であり、
\end{equation}

\[
\mathrm{det}T = |T| = \left|
\begin{array}{ccc}
1 – λ & 2 & 0 \\
2 & 1 – λ & 0 \\
0 & 0 & 3 – λ
\end{array}
\right| = 0
となればいいことがわかる。
\]

\begin{equation}
= (1 – λ)^2 (3 – λ) – 4 (3 – λ)
\end{equation}

\begin{equation}
= (1 – 2λ + λ^2)(3 – λ) – 12 + 4λ
\end{equation}

\begin{equation}
= -λ^3 + 5λ^2 – 3λ – 9 = 0
\end{equation}

\begin{equation}
λ^3 – 5λ^2 + 3λ + 9 = 0
\end{equation}

\begin{equation}
(λ + 1)(λ^2 – 6λ + 9) = 0
\end{equation}

\begin{equation}
(λ + 1)(λ – 3)^2 = 0
\end{equation}

\begin{equation}
よって、固有値はλ = -1,3
\end{equation}

次にそれぞれの固有値における固有ベクトルを求めます。
\begin{equation}
ⅰ)λ = -1の時、①をT_{1}X_{1}=0,
\end{equation}
\[
X_{1}=\left(
\begin{array}{ccc}
α_{1} \\
α_{2} \\
α_{3}
\end{array}
\right)
とすると、
\]

\[
\left(
\begin{array}{ccc}
2 & 2 & 0\\
2 & 2 & 0 \\
0 & 0 & 4
\end{array}
\right)
\left(
\begin{array}{ccc}
α_{1}\\
α_{2}\\
α_{3}
\end{array}
\right)
= \left(
\begin{array}{ccc}
0\\
0\\
0
\end{array}
\right)
\]

\begin{eqnarray}
\begin{cases}
2α_{1} + 2α_{2} = 0 & \\
4α_{3} = 0
\end{cases}
\end{eqnarray}

\begin{equation}
α_{1}=k_{1}とすると、α_{2}=-k_{1}より、固有ベクトルX_{1}は
\end{equation}

\[
X_{1}=k_{1}\left(
\begin{array}{ccc}
1 \\
-1 \\
0
\end{array}
\right)
（k_{1}\neq0）
\]

\begin{equation}
ⅱ)λ = 3の時、①をT_{2}X_{2}=0,
\end{equation}
\[
X_{2}=\left(
\begin{array}{ccc}
α_{4} \\
α_{5} \\
α_{6}
\end{array}
\right)
とすると、
\]

\[
\left(
\begin{array}{ccc}
-2 & 2 & 0\\
2 & -2 & 0 \\
0 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{ccc}
α_{4}\\
α_{5}\\
α_{6}
\end{array}
\right)
= \left(
\begin{array}{ccc}
0\\
0\\
0
\end{array}
\right)
\]

\begin{eqnarray}
\begin{cases}
-2α_{4} – 2α_{5} = 0 & \\
α_{6} = k_{3}
\end{cases}
\end{eqnarray}

\begin{equation}
α_{4}=k_{2}とすると、α_{5}=-k_{2}より、固有ベクトルX_{2}は
\end{equation}

\[
X_{2}=k_{2}\left(
\begin{array}{ccc}
1 \\
-1 \\
0
\end{array}
\right)
+k_{3}\left(
\begin{array}{ccc}
0 \\
0 \\
1
\end{array}
\right)
（k_{2},k_{3}\neq0）
\]

以上、ⅰ），ⅱ）より、
\[
変換行列P= \left(
\begin{array}{ccc}
1 & 1 & 0 \\
-1 & -1 & 0 \\
0 & 0 & 1
\end{array}
\right)
とおくと、対角化した行列は
\]

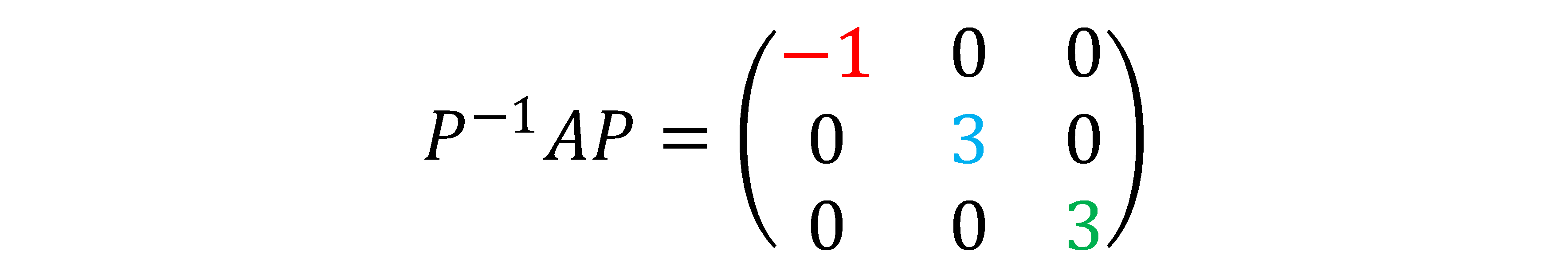
「あれっ？なんで急に対角化出来たん！？」って思いませんでした？
普通に考えると【院試対策】線形代数③（行列の和積）で紹介したように“行列の積”を用いて解くことになりますが、実は行列の対角化には秒で求めることが出来る公式があります♪それがこちら↓

【対角化の公式】
\begin{equation}
それぞれの固有値の線形独立な固有ベクトルがX_{1},X_{2},X_{3},・・・,X_{n}である時、
\end{equation}
\begin{equation}
変換行列P=(X_{1},X_{2},X_{3},・・・,X_{n})を用いると、対角行列は固有値λ_{1},λ_{2},・・・,λ{n}を用いて、
\end{equation}

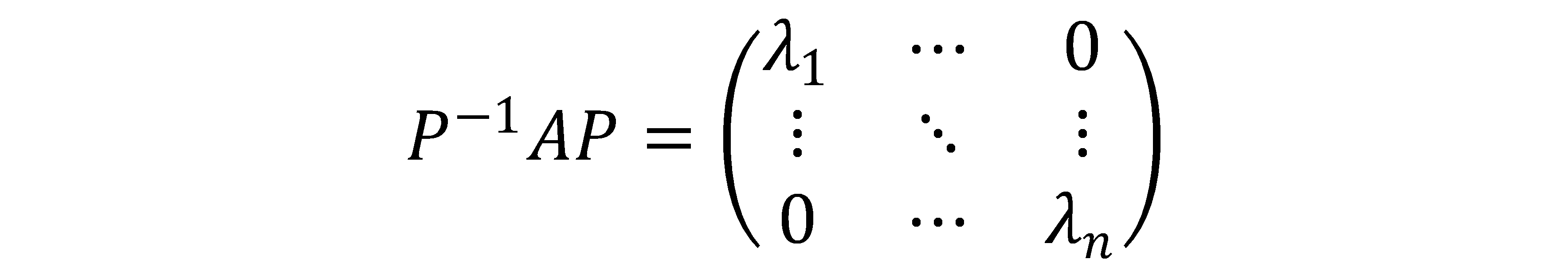
いかがでしたでしょうか？

この数式を書くのが中々時間がかかるので１問しか紹介できませんでしたが、上の例題で示した解法が行列の固有値と固有ベクトルの基本的な求め方となります。

今回はただの変換行列を用いた対角化を紹介しましたが、次回は変換行列に直交行列を用いた特殊パターンについて紹介いたします。

p.s.実は今回の変換行列も直交行列にしてしまっていたので、次回は固有ベクトルの段階では直交行列でないものをシュミットの正規直交化法を用いて無理やり、直交行列にして対角化をするというものを扱います！

お楽しみに♪

▲▲▲ｱﾘｶﾞ島▲▲▲