【院試対策】線形代数③（行列の和積）

こんにちは～

前回の予告通り、今回は“行列の和積”の計算の仕方について記事にしていきたいと思います。

それでは～

シュワッチ！

---

 

第３回：【院試対策】線形代数③（行列の和積）

第３回は“行列の和積”についてです。
前回までは“同時連立１次方程式”と”非同次連立１次方程式”という連立１次方程式の解き方を紹介しましたが、今回は行列の和積の解き方を紹介したいと思います！

“行列の和積”も僕の大学では頻出の問題となっています。

＜例題＞
行列J,Kを

\[
J = \left(
\begin{array}{ccc}
0 & 0 & 1\\
1 & -1 & 0\\
1 & 0 & -1
\end{array}
\right)
\]
\[
K = \left(
\begin{array}{ccc}
0 & 0 & 1\\
0 & -1 & 0\\
1 & 0 & -1
\end{array}
\right)
\]

とおく。\begin{eqnarray*}
&& J^2とJK+KJを求めよ。
\end{eqnarray*}

＜解法＞
（１）

 

\[
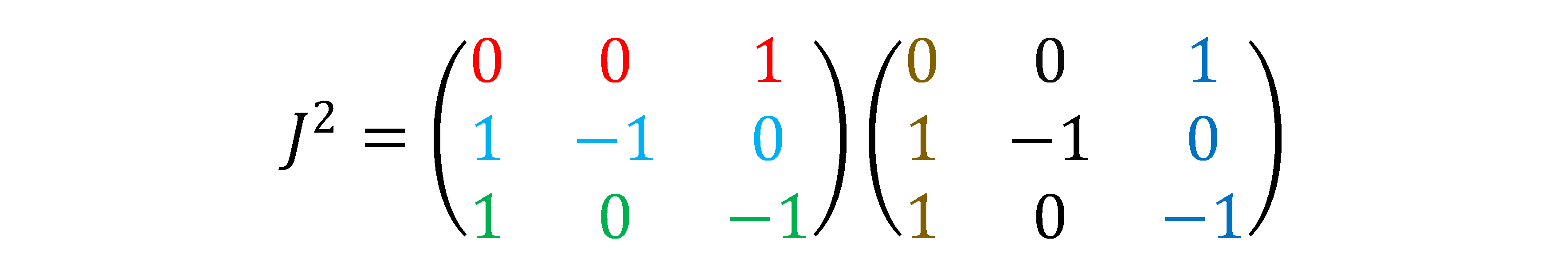
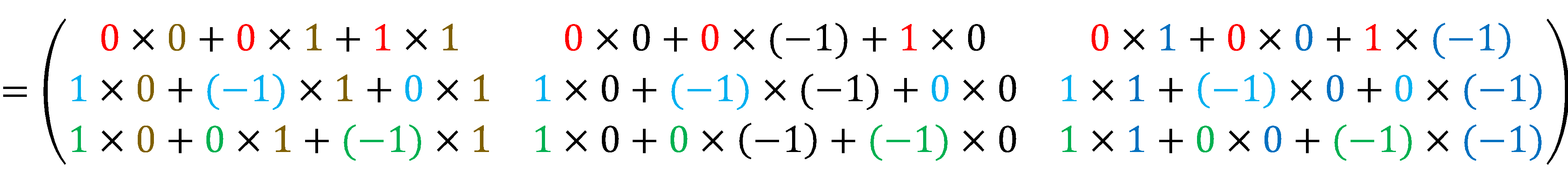
=\left(
\begin{array}{ccc}
1 & 0 & -1\\
-1 & 1 & 1\\
-1 & 0 & 2
\end{array}
\right)
\]

（２）

\[
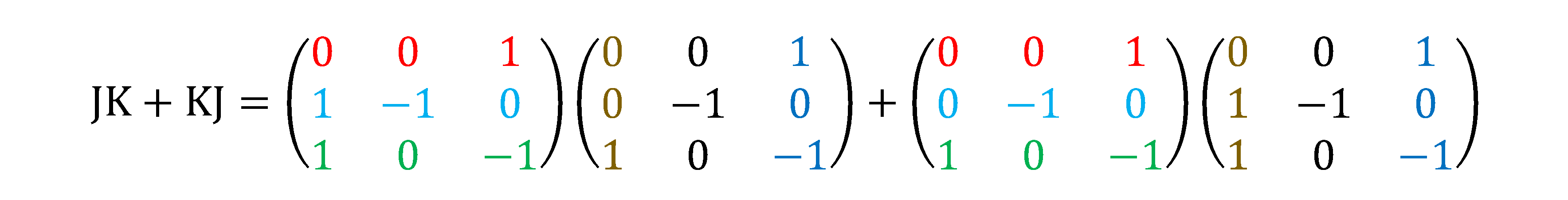
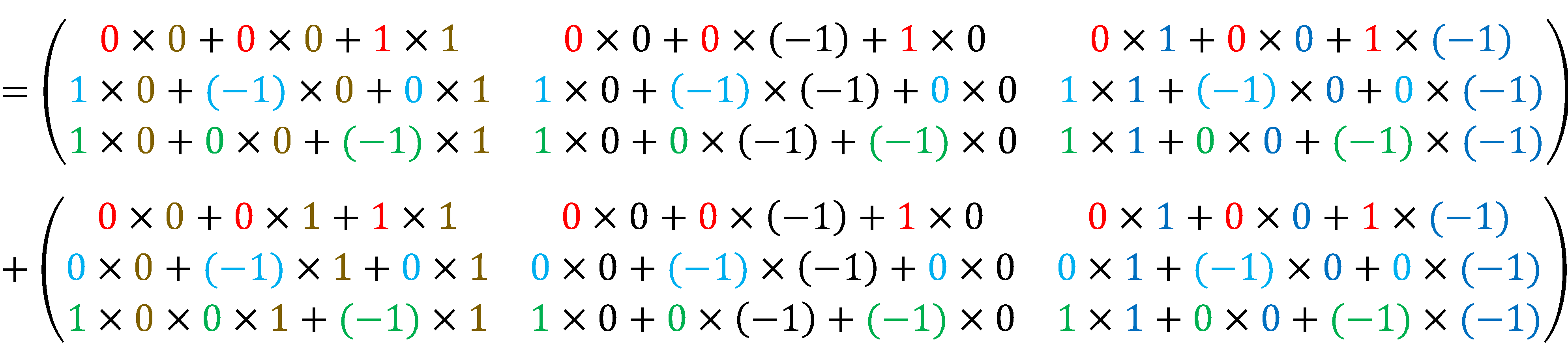
=\left(
\begin{array}{ccc}
1 & 0 & -1\\
0 & 1 & 1\\
-1 & 0 & 2
\end{array}
\right)
+\left(
\begin{array}{ccc}
1 & 0 & -1\\
-1 & 1 & 0\\
-1 & 0 & 2
\end{array}
\right)
\]

\[
=\left(
\begin{array}{ccc}
1+1 & 0+0 & -1-1\\
0-1 & 1+1 & 1+0\\
-1-1 & 0+0 & 2+2
\end{array}
\right)
\]

\[
=\left(
\begin{array}{ccc}
2 & 0 & -2\\
-1 & 2 & 1\\
-2 & 0 & 4
\end{array}
\right)
\]

---