【院試対策】線形代数④（行列の固有値と固有ベクトル）

こんにちは～

前回の予告通り、今回は“行列の固有値と固有ベクトル”の求め方について記事にしていきたいと思います。

それでは～

シュワッチ！

---

 

第４回：【院試対策】線形代数④（行列の固有値と固有ベクトル）

第4回は”行列の固有値と固有ベクトル”についてです。
まず、「固有値と固有ベクトルとは何ぞや？」と思いますよね！

なので、定義から↓

これだけではイメージがつきにくいと思うので、固有ベクトルについての詳細を↓

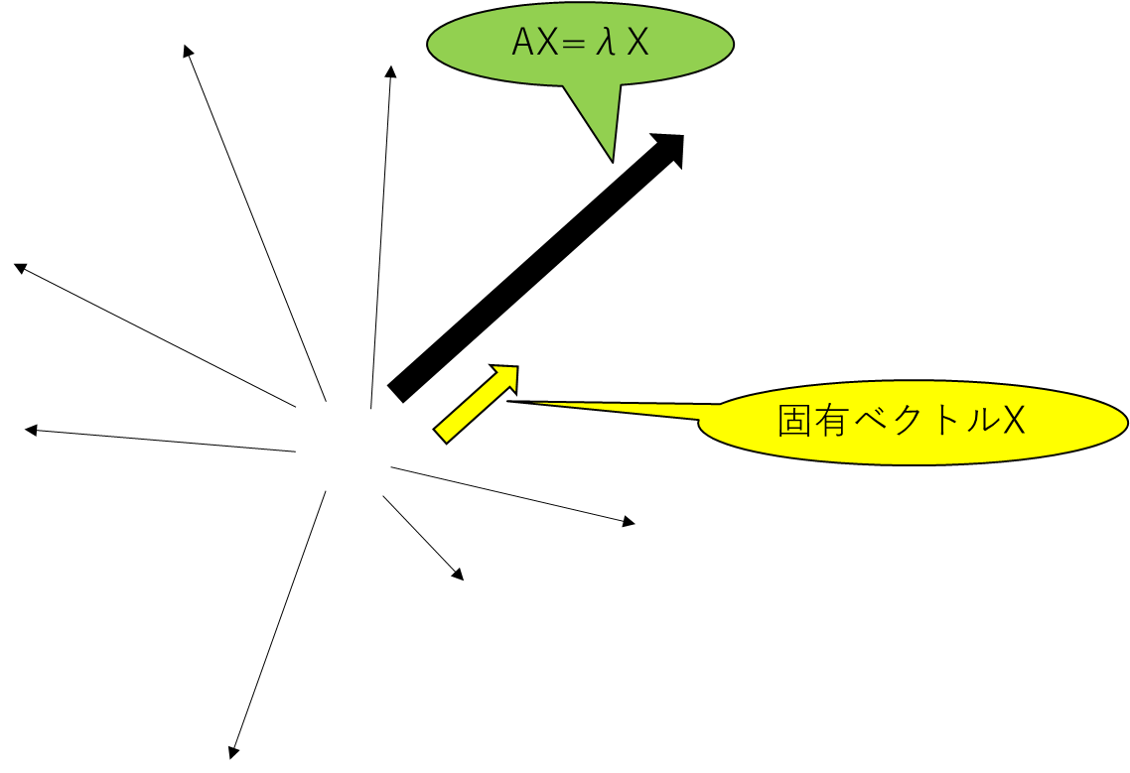
普通、ベクトル同士を掛けたもの（AX）はベクトルXとは違う方向になる事がほとんど。
その中で、ベクトル同士の掛け算を行っても奇跡的にオリジナルのベクトルXと方向が一致するベクトルが固有ベクトルなのです！

どうです？なんか、素敵じゃないですか（笑）

定義を説明した所で、例題を使って実践演習をしていきましょう！

＜例題１＞
以下の行列Aの固有値と固有ベクトルを求めよ。
\[
A = \left(
\begin{array}{ccc}
1 & 2 & 0 \\
2 & 1 & 0 \\
0 & 0 & 3
\end{array}
\right)
\]

＜解法＞
\begin{equation}
AX = λX　より、（A – λE）X = 0
\end{equation}

\[
ここで、T = A – λE = \left(
\begin{array}{ccc}
1 & 2 & 0 \\
2 & 1 & 0 \\
0 & 0 & 3
\end{array}
\right)
– \left(
\begin{array}{ccc}
λ & 0 & 0 \\
0 & λ & 0 \\
0 & 0 & λ
\end{array}
\right)
\]

\[
= \left(
\begin{array}{ccc}
1-λ & 2 & 0 \\
2 & 1-λ & 0 \\
0 & 0 & 3-λ
\end{array}
\right)
とおく。
\]

\begin{equation}
すると、TX = 0・・・①であり、
\end{equation}

\[
\mathrm{det}T = |T| = \left|
\begin{array}{ccc}
1 – λ & 2 & 0 \\
2 & 1 – λ & 0 \\
0 & 0 & 3 – λ
\end{array}
\right| = 0
となればいいことがわかる。
\]

\begin{equation}
= (1 – λ)^2 (3 – λ) – 4 (3 – λ)
\end{equation}

\begin{equation}
= (1 – 2λ + λ^2)(3 – λ) – 12 + 4λ
\end{equation}

\begin{equation}
= -λ^3 + 5λ^2 – 3λ – 9 = 0
\end{equation}

\begin{equation}
λ^3 – 5λ^2 + 3λ + 9 = 0
\end{equation}

\begin{equation}
(λ + 1)(λ^2 – 6λ + 9) = 0
\end{equation}

\begin{equation}
(λ + 1)(λ – 3)^2 = 0
\end{equation}

\begin{equation}
よって、固有値はλ = -1,3
\end{equation}

次にそれぞれの固有値における固有ベクトルを求めます。
\begin{equation}
ⅰ)λ = -1の時、①をT_{1}X_{1}=0,
\end{equation}
\[
X_{1}=\left(
\begin{array}{ccc}
α_{1} \\
α_{2} \\
α_{3}
\end{array}
\right)
とすると、
\]

\[
\left(
\begin{array}{ccc}
2 & 2 & 0\\
2 & 2 & 0 \\
0 & 0 & 4
\end{array}
\right)
\left(
\begin{array}{ccc}
α_{1}\\
α_{2}\\
α_{3}
\end{array}
\right)
= \left(
\begin{array}{ccc}
0\\
0\\
0
\end{array}
\right)
\]

\begin{eqnarray}
\begin{cases}
2α_{1} + 2α_{2} = 0 & \\
4α_{3} = 0
\end{cases}
\end{eqnarray}

\begin{equation}
α_{1}=k_{1}とすると、α_{2}=-k_{1}より、固有ベクトルX_{1}は
\end{equation}

\[
X_{1}=k_{1}\left(
\begin{array}{ccc}
1 \\
-1 \\
0
\end{array}
\right)
（k_{1}\neq0）
\]

\begin{equation}
ⅱ)λ = 3の時、①をT_{2}X_{2}=0,
\end{equation}
\[
X_{2}=\left(
\begin{array}{ccc}
α_{4} \\
α_{5} \\
α_{6}
\end{array}
\right)
とすると、
\]

\[
\left(
\begin{array}{ccc}
-2 & 2 & 0\\
2 & -2 & 0 \\
0 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{ccc}
α_{4}\\
α_{5}\\
α_{6}
\end{array}
\right)
= \left(
\begin{array}{ccc}
0\\
0\\
0
\end{array}
\right)
\]

\begin{eqnarray}
\begin{cases}
-2α_{4} – 2α_{5} = 0 & \\
α_{6} = k_{3}
\end{cases}
\end{eqnarray}

\begin{equation}
α_{4}=k_{2}とすると、α_{5}=-k_{2}より、固有ベクトルX_{2}は
\end{equation}

\[
X_{2}=k_{2}\left(
\begin{array}{ccc}
1 \\
-1 \\
0
\end{array}
\right)
+k_{3}\left(
\begin{array}{ccc}
0 \\
0 \\
1
\end{array}
\right)
（k_{2},k_{3}\neq0）
\]

\begin{equation}
＊ちなみにλが重解である固有ベクトルX_{2}は以下のように分けることが出来、互いに線形独立です。
\end{equation}

\[
X_{2}’=k_{2}\left(
\begin{array}{ccc}
1 \\
-1 \\
0
\end{array}
\right)
,X_{2}”=k_{3}\left(
\begin{array}{ccc}
0 \\
0 \\
1
\end{array}
\right)
\]

---

 

いかがでしたでしょうか？

この数式を書くのが中々時間がかかるので１問しか紹介できませんでしたが、上の例題で示した解法が行列の固有値と固有ベクトルの基本的な求め方となります。

それでは、次回は今回導いた固有値と固有ベクトルを用いれば“行列の対角化”が出来るので、その方法について紹介いたします。

お楽しみに♪

▲▲▲ｱﾘｶﾞ島▲▲▲